Bitcoin Magazine
How CoinJoin Anonymity Can Be Undermined Using Clustering
Anonymity is the end goal when studying privacy, and it’s useful to think of de-anonymization as a game.
We imagine an adversary with some access to information, and it tries to guess correctly who among a set of candidates was responsible for some event in the system. To defend against the adversary winning, we need to keep it guessing, which could either mean limiting its access to information or using randomness to increase the amount of information it needs to succeed.
Many readers will be familiar with the game of “Guess Who?”. This game could be described as a turn-based composition of two instances of the more general game “twenty questions.” In “twenty questions,” you secretly choose an element from a given set, and your opponent tries to guess it correctly by asking you up to 20 yes-or-no questions. In “Guess Who?” both sides take turns playing against each other, and the first to guess correctly wins. The set of elements is fixed in “Guess Who?”, consisting of 24 cartoon characters with various distinguishing features, such as their hair color or style. Each character has a unique name that unambiguously identifies them.
The answers to a yes-or-no question can be represented as a bit — zero or one. Twenty bits can express, in base 2, any whole number in the range 0 to 1,048,575, which is 2²⁰-1. If a set can be totally ordered, each element in the set may be indexed by its numbered position in the order, which uniquely identifies it. So, 20 bits can uniquely address one of just over a million elements.
Although 2²⁰ is the maximum number of elements of a set that could be uniquely identified using just the answers to 20 yes-or-no questions, in real-world situations, 20 answers will often contain less information than that. For most sets and combinations of questions, things will almost certainly not line up perfectly, and not every question will bisect the candidate elements independently of the other questions. The answers to some questions might be biased; some questions’ answers might correlate with those of other questions.
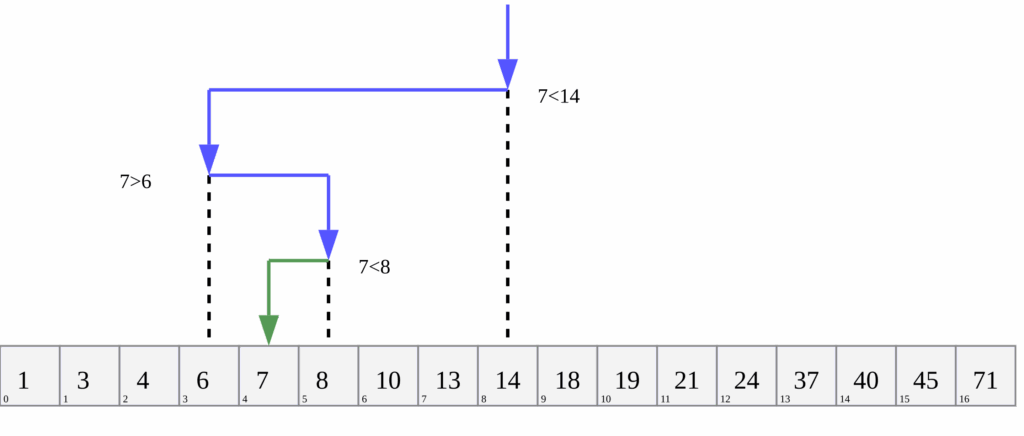
Suppose that instead of asking something like “does your character have glasses?” you always ask, “Alphabetically, does your character’s name appear before [median remaining character’s name]?”. This is a binary search, which will maximize how informative the answer to each question will be: At every step, the median name partitions the set of remaining characters, and the question eliminates one of the two halves. Repeatedly halving the remaining candidates will narrow down the search as quickly as yes-or-no answers make possible; only a logarithmic number of steps is required, which is much faster than, say, a linear scan (i.e., checking one by one: “Is it Alice? No? How about Bob? …”).
Bear in mind that if you are playing to win, the point of the game is not to get the most information out of your opponent but to be the first to guess correctly, and it turns out that maximizing the information per answer is actually not the optimal strategy — at least when the game is played honestly. Similarly, when using games to study privacy, one must assume the adversary is rational according to its preferences; it’s fairly easy to accidentally optimize for a subtly incorrect outcome, since the adversary is playing to win.
Finally, suppose the players are no longer assumed to be honest. It should be apparent that one can cheat without getting detected; instead of choosing an element of the set at the start and then answering honestly in response to every question, you can always give the answer that would leave the largest number of remaining candidates. Adaptively chosen answers can therefore minimize the rate at which one’s opponent obtains useful information to win the game. In this so-called Byzantine setting, the optimal strategy is no longer the same as when players are honest. Here, an opponent’s best response would be to stick with binary search, which limits the advantage of playing adaptively.
Adaptive “Guess Who?” is pretty boring, similar to how tic-tac-toe should always end in a draw if you’re paying attention. To be precise, as we will see in the next section, there are 4.58 bits of information to extract from your maximally adversarial opponent, and the rules of the game can be used to force the opponent to commit to those bits. This means the first player can always win after five questions. The transcript of answers in such games should always consist of uniformly random bits, as anything else would give an edge to one’s opponent. Unfortunately, privacy protections using such adaptivity or added randomness are difficult to build and understand, so actual privacy software is usually significantly harder to analyze than these toy examples.
Measuring Anonymity: Shannon Entropy
The information content of an answer in “Guess Who?” — also known as its Shannon entropy — quantifies how surprising it is to learn. For example, if you already found out that your opponent’s character is bald, it won’t surprise you to learn that they do not have black hair; this answer contains no additional information. This wasn’t surprising because, before being told, you could infer that the probability of having black hair was zero.
Suppose that two options remain from the set of candidates; it’s basically a coin toss, and either of the two options should be equally likely and, therefore, equally surprising. Learning that it’s option A tells you it isn’t B — equivalently, learning that it’s not B tells you that it must be A — so only one yes-or-no question, one bit of information, is needed to remove all uncertainty.
This value can be calculated from the probability distribution, which in this binary example is Bernoulli with p=1/2.
First, compute the negation of the base 2 logarithm of the probability of each case, or equivalently invert the probability first and skip the negation:
First, compute the negation of the base 2 logarithm of the probability of each case, or equivalently invert the probability first and skip the negation:
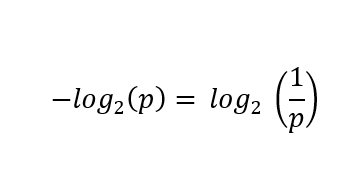
In both cases:
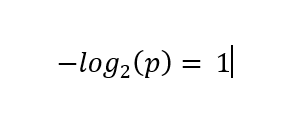
These values are then scaled by multiplying these values by their corresponding probabilities (as a sort of weighted average), resulting in a contribution of ½ bits for either case. The sum of these terms, 1 in this case, is the Shannon entropy of the distribution.
This also works with more than two outcomes. If you start the game by asking, “Is it [a random character’s name]?” you will most likely only learn
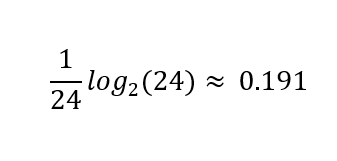
bits of information if the answer was “no.”
At that point log₂(23) ≈ 4.52 bits quantify your remaining uncertainty over the 23 equally likely remaining possibilities. On the other hand, if you were lucky and guessed correctly, you will learn the full log₂(24) ≈ 4.58 bits of information, because no uncertainty will remain.
Just under 5 bits are needed to narrow down to one of 24 characters. Ten bits can identify one in 1,024; 20 bits, around one in a million.
Shannon entropy is general enough to quantify non-uniform distributions, too. Not all names are equally popular, so an interesting question is, “How much entropy is in a name“? The linked post estimates this at roughly 15 bits for U.S. surnames. According to another paper, first names in the U.S. contain approximately 10-11 bits. These estimates imply an upper bound of 26 bits per full name, but remember that a common name like John Smith will contain less information than an uncommon one. (Uniquely addressing the entire U.S. population requires 29 bits.)
As of writing, the world population is slowly but surely approaching 8.5 billion, or 2³³ people. Thirty-three is not a very large number: How many bits are in a birthdate? Just an age? Someone’s city of residence? An IP address? A favorite movie? A browser’s canvas implementation? A ZIP code? The words in their vocabulary, or the idiosyncrasies of their punctuation?
These are tricky questions. Unlike these games and modern cryptography, where secrets are random and preferentially ephemeral, we can’t randomize, expire or rotate our real-life identifying attributes.
Furthermore, this personally identifying information often leaks both by necessity and sometimes unnecessarily and unintentionally throughout our lives. We often have to trust people with whom we interact not to reveal this information, whether by sharing it with third parties or accidentally leaking it. Perhaps it’s not unlike how we must trust others with our lives, like doctors or professional drivers and pilots. Still, certainly it is not comparable in terms of how necessary it is to trust as a matter of course when it comes to our personal data.
An Entropist Perspective on Anonymity
Privacy-enhanced systems allow users to hide in a crowd. For example, if you observe a connection to your server from a Tor exit node, for all you know, it’s one of potentially thousands of Tor users that established that connection. Informally, given some event that a deanonymization adversary has observed — perhaps by intercepting a message being transmitted between two nodes in a network — a particular user’s anonymity set refers to the set of potential users to whom that event might be attributed.
If the receiver of an anonymous message is taken to be the adversary, then their best guess from a set of candidate senders is the sender’s anonymity set. If this hypothetical system is fully anonymous, then any user is equally likely to have sent the message, apart from the receiver.
Two influential papers that proposed to measure anonymity in terms of the entropy of the anonymity set were published concurrently: “Towards Measuring Anonymity” by Claudia Díaz, Stefaan Seys, Joris Claessens and Bart Preneel, and “Towards an Information Theoretic Metric for Anonymity” by Andrei Serjantov and George Danezis. These works generalize from the assumption that the adversary can guess the correct user from an anonymity set no better than chance, to a model that accounts for nonuniform probability distributions over this set. Both propose the quantification of anonymity set sizes in terms of bits of entropy.
When the anonymity set is perfectly symmetric, only the uniform distribution makes sense, so converting the anonymity set size to bits is just a matter of computing a log₂(n) where n is the size of the set. For example, 1024 equiprobable elements in a set have 10 bits of entropy in their distribution.
When the distribution is not uniform, the entropy of the distribution decreases. For example, if either heads or tails is possible, but there’s a ¼ probability of heads, ¾ of tails, the total entropy of this distribution is only
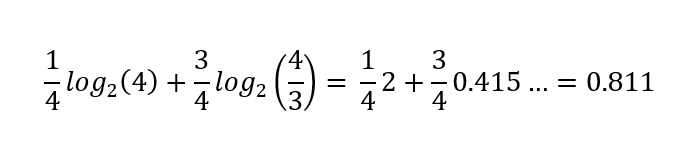
bits instead of a full bit. This quantifies the uncertainty represented in a probability distribution; the outcome of flipping this bent coin is comparatively less uncertain than that of a fair coin.
Shannon entropy is a special case of an entire family of entropy definitions. It characterizes the average information content in a message (a yes-or-no answer, or more generally) drawn from a probability distribution over possible messages. A more conservative estimate might use min-entropy, which considers only the highest probability element instead of calculating the arithmetic mean, quantifying the worst-case scenario. In this post, we’ll stick to Shannon entropy. For a more in-depth discussion and a nuanced interpretation of the entropist perspective, Paul Syverson’s “Why I’m not an Entropist” is a thoughtful read.
Anonymity Intersections
In k-anonymity: a model for protecting privacy, Latanya Sweeney reviews some of her prior results as motivation — results which demonstrated re-identification of “anonymized” data. Individually, each attribute in a data set associated with an entry, such as a date of birth, might seem to reveal very little about the subject of that entry. But like the yes-or-no questions from the game, only a logarithmic amount of information is needed; in other words, combinations of surprisingly small numbers of attributes will often be sufficient for re-identification:
For example, a finding in that study was that 87% (216 million of 248 million) of the population in the United States had reported characteristics that likely made them unique based only on {5-digit ZIP, gender, date of birth}. Clearly, data released containing such information about these individuals should not be considered anonymous.
As a rough estimate, a string of 5 digits would have log₂(10⁵) ≈ 16.6 bits of max entropy, but there are fewer ZIP codes than that, log₂(4.3 x 10⁴) ≈ 15.4 — and keep in mind that the population is not uniformly distributed over ZIP codes, so 13.8 would be a better estimate. A gender field would usually contain slightly more than 1 bit of information in most circumstances, because even if nonbinary genders are represented, the majority of entries will be male or female. That said, entries with nonbinary values would reveal a lot more than 1 bit about the subject of that entry. A date of birth is also tricky to estimate without looking at the distribution of ages.
Ignoring February 29 and assuming uniformly distributed birthdays and 2-digit birth year, the entropy would be log₂(365 x 10²) ≈ 15.1. Again, a more realistic estimate is available, 14.9 bits. Taken together, the more conservative estimates total roughly 29.7 bits. For comparison, the entropy of a uniform distribution over the U.S. population at the time is log₂(248 x 10⁶) ≈ 27.9 bits, or log₂(342 x 10⁶) ≈ 28.4 with up-to-date figures.
The following diagram from the paper will probably look familiar to anyone who has spent some time learning what an “inner join” is in SQL. It illustrates a different example where Sweeney linked medical records to the voter registration list using the same fields, identifying then-Massachusetts Governor William Weld’s specific record in an “anonymized” medical dataset:
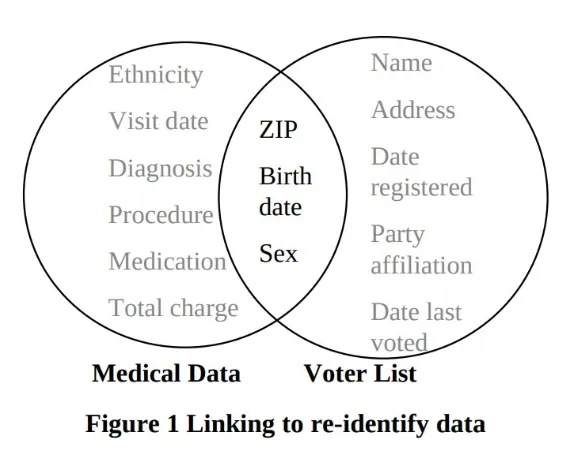
This kind of Venn diagram, with two sets represented by two overlapping circles and the overlapping part highlighted, typically represents an intersection between two sets. Sets are unordered collections of elements, such as rows in a database, numbers, or anything else that can be mathematically defined. The intersection of two sets is the set of elements that are present in both sets. So, for example, within the voter registration list, we might talk about the subset of all entries whose ZIP code is 12345, and the set of all entries whose birth date is January 1, 1970. The intersection of these two subsets is the subset of entries whose ZIP code is 12345 and whose date of birth is January 1, 1970. In the governor’s case, there was just one entry in the subset of entries whose attribute values matched his attributes in the voter registration list.
For data sets with different structures, there’s a small complication: If we think of them as sets of rows, then their intersection would always be empty, because the rows would have different shapes. When computing the inner join of two database tables, only the values of columns that are present in both tables are in some sense intersected by specifying something like JOIN ON a.zip = b.zip AND a.dob = a.dob, or the less portable USING(zip, dob) syntax, but these intersecting values are related to the rows they came from, so the overall structure of linking two data sets is a bit more involved.
Note that Sweeney’s diagram depicts the intersection of the columns of the data sets, emphasizing the more primary problem, which is that attributes included in the “anonymized” data set unintentionally had a non-empty intersection with the attributes of other publicly available data sets.
On the applied side of the k-anonymity model, the procedures for anonymizing datasets described in the paper have fallen out of favor due to some weaknesses discovered in subsequent work (“Attacks on Deidentification’s Defenses” by Aloni Cohen). That central idea in k-anonymity is to ensure that for every possible combination of attributes, there are at least k rows containing every specific combination in the data, which suggests log₂(k) additional bits of information would be needed to identify an entry from its congruent ones. The deidentification procedure suggested for ensuring this was the case was to redact or generalize in a data-dependent way, for example, drop the day from a date of birth, keeping the year and month, or even only the year, if that’s not enough. Cohen’s work shows how easy it is to underestimate the brittleness of privacy, because even discarding information until there’s k of every combination, the redaction process itself leaks information about the statistics of the unredacted data set. Such leaks, even if very subtle, will not only add up over time, but they will typically compound. Accounting for privacy loss using bits, which are a logarithmic scale, perhaps helps provide a better intuition for the typically exponential rate of decay of privacy.
Anonymity in Bitcoin CoinJoins: Intersection Attacks
In their paper “When the Cookie Meets the Blockchain: Privacy Risks of Web Payments via Cryptocurrencies,” Steven Goldfeder, Harry Kalodner, Dillon Reisman and Arvind Narayanan describe two independent but related attacks. Perhaps more importantly, they also make a very compelling case for the brittleness of privacy more broadly, by clearly demonstrating how privacy leaks can compound.
In Bitcoin, a natural definition of an anonymity set for a coin is the set of wallet clusters into which the coin could plausibly be merged. The anonymity set is nontrivial if there is more than one candidate cluster, in which case merging would be contingent on obtaining additional information. New transactions might introduce uncertainty, necessitating the creation of new clusters for outputs that can’t be merged into any existing cluster (yet). On the other hand, new transactions and out-of-band information can also remove uncertainty and facilitate the merging of clusters. Most commonly, if the multi-input heuristic is considered valid for such a new transaction, then the clusters of the input coins will be merged. However, as we saw before, many heuristics exist, some of which are alarmingly accurate.
Suppose that Alice received some bitcoin into a wallet under her control. Some might have been withdrawn from an exchange (presumably with KYC information). Maybe a friend paid her back for lunch. Maybe she sold her car. After making several transactions, Alice realizes that her transaction history is visible to all and pretty straightforward to interpret, but soon she will need to make not just one, but two separate transactions, with stronger privacy assurances than she has been relying on so far.
After learning a bit about privacy, Alice decides to use a wallet that supports CoinJoin. Over several CoinJoin transactions, she spends her existing coins, obtaining replacement coins that apparently have a non-trivial anonymity set. Before CoinJoining, her wallet was likely clusterable. After CoinJoining, each UTXO she now has can’t be assigned to any specific cluster, since other users’ wallet clusters are also implied in the various CoinJoin transactions.
The intuition behind CoinJoin privacy is that since multiple inputs belonging to different users are used to create outputs that all look the same, no one output can be linked to a specific input. This is somewhat analogous to a mixnet, where each CoinJoin transaction is a relay and the “messages” being mixed are the coins themselves. This analogy is very simplistic, there are many complications when implementing CoinJoins that cause it to break down, but we will ignore these nuances in this post and give Alice’s chosen CoinJoin wallet the benefit of the doubt and assume that Alice can always successfully spend just one input into each CoinJoin, and that this results in perfect mixing of her funds with those of the other parties to the CoinJoin. Under these assumptions, if there are k equivalent outputs in a CoinJoin transaction, and k separate clusters for the inputs, then each output’s anonymity set should have log₂(k) bits of entropy when this transaction is created.
Post-CoinJoin Clustering
The stage is now set for the first attack described in the paper. This attack was made possible by inclusion of third party resources, e.g., a payment processor’s javascript on merchant websites. Supposing the payment address used for the transaction is revealed to the third party, that would link Alice’s web session to her on-chain transaction. The paper is from 2017, so the specifics of web-related leaks are somewhat dated by now, but the principle underlying this concern is as relevant as ever.
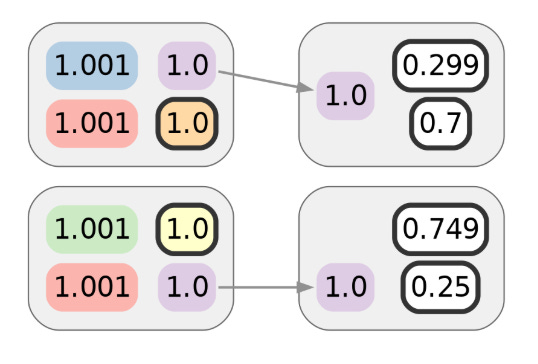
Alice uses one of her CoinJoin UTXOs to make the first of those privacy-demanding transactions. Assuming no semantic leaks (such as a billing address related to a purchase) or metadata leaks (perhaps she broadcasts using Tor), this transaction should preserve the privacy Alice obtained from the prior CoinJoin transaction. As drawn here, that would be 1 bit’s worth. The colors of inputs or outputs indicate the cluster they are already assigned to. Alice’s coins are in red, and gradients represent ambiguity:
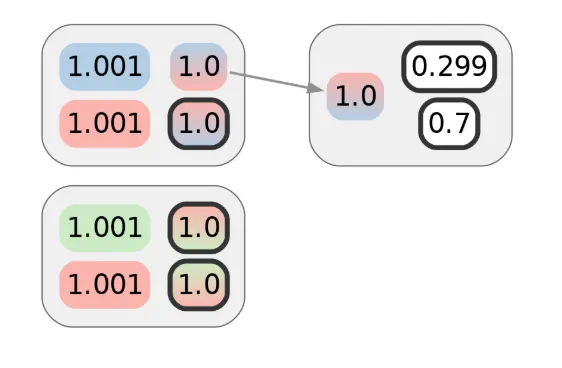
While the first transaction does not reveal much on its own, suppose Alice makes another transaction. Let’s say it’s with a different merchant, but one that uses the same payment processor as the first merchant. Naively, it would appear that the following diagram represents the privacy of Alice’s payment transactions, and that the adversary would need 2 bits of additional information — 1 for each transaction — to attribute them both to Alice’s cluster:
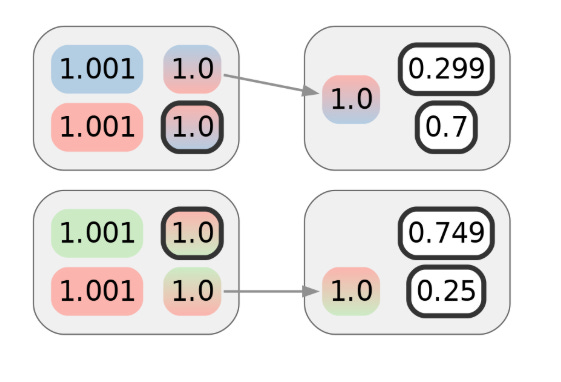
Although Alice intends this to be unlinkable to the first transaction, she might not realize her web browsing activity is being tracked. The paper showed that this kind of tracking was not just possible but even practical, and can reveal to a third party that the two transactions can be clustered even though they don’t appear related on-chain. Visually, we can represent this clustering with additional colors:
Web tracking, as discussed in the paper, is just one of many ways information that facilitates clustering can leak. For example, website breaches can result in purchase records being made public, even years after the fact. In at least one example, legal proceedings, which are supposed to protect victims, ended up exposing them to even more harm by needlessly revealing information about the on-chain transactions of customers through improper redaction of the transacted amounts. The previous post on the history of wallet clustering provides several additional examples.
Specifically in the context of CoinJoins, a typical way that this sort of linkage could occur is when the change outputs of post-mix payment transactions are subsequently CoinJoined in a manner that causes them to be linkable by clustering the inputs. This is also known as the toxic change problem, which is illustrated in the next diagram. Note that white doesn’t represent a single cluster, just lack of clustering information in this example.
If the coordinator of the supposedly “trustless” CoinJoin protocols is malicious, then even attempting to CoinJoin may link the transactions, even if this doesn’t become self-evident on-chain. The consequences are the same as the attack described in the paper, except that a CoinJoin coordinator can also pretend that some participants failed to submit their signatures in time, actively but covertly, or at least deniably disrupting rounds to obtain more clustering information.
Intersection Antecessor Clusters
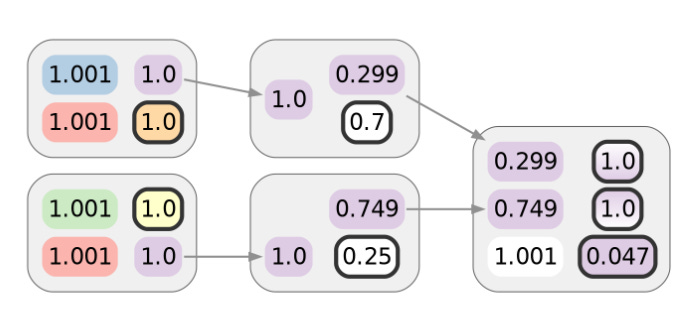
Unfortunately for Alice, the story doesn’t end there. What the paper showed next was that given such linking of post-CoinJoin transactions, regardless of how this clustering was learned, an intersection attack on the privacy of the CoinJoin transactions themselves also becomes possible.
It’s as if the adversary is playing “Guess Who?” and is given a payment transaction, then tries to guess where the funds originated from. Consider the set of inputs for each CoinJoin transaction. Every one of the spent coins is assigned to some cluster. Every one of the CoinJoin transactions Alice participated in has an input that is linkable to one of her clusters. The privacy of such transactions derives from being linked to a large number of otherwise unrelated clusters. Armed with knowledge that post-CoinJoin transactions link multiple CoinJoin outputs together, the adversary can compute the intersection of the sets of associated clusters. How often will it be the case that a random individual user participated in every transaction that Alice did? What about more than one? Not very often. And suppose the intersection contains a unique cluster, which could often eventually be the case. In that case, the adversary will be able to link Alice’s transactions to each other and her pre-CoinJoin transaction history, effectively undoing the mix.
Visually, this combines the inferences of previous diagrams. For each coin in the purple cluster of the last two diagrams, we can intersect the sets of colors in the gradients depicted in the diagram before that:

Only Alice’s red cluster is in the intersection, so that the purple cluster can be merged into the red one. Not only do Alice’s clusters merge, since this example only has two user CoinJoin transactions, the remaining clusters can also be merged with their ancestors by process of elimination, so Alice’s linkable payments would also potentially deanonymize a hypothetical Bob and Carol in this particular case:

This suggests that even if CoinJoins functioned like a perfect mix (which they don’t), insufficient post-mix transaction privacy can additionally undermine the privacy of the prior CoinJoin transactions, and much more rapidly than seems intuitive. The graph structure, which connects Bitcoin transactions, contains a wealth of information available to a deanonymization adversary.
Privacy concerns are often downplayed, perhaps due to defeatist attitudes in light of the challenges of preventing or even controlling privacy leaks. Hopefully awareness will improve, and things will play out like they did in cryptography in previous decades — whether it’s no longer shipping weak “export” crypto, or how timing side channels were mostly ignored at first, but are now widely understood to be practically exploitable and implementations that don’t take them into account are considered insecure. That said, it’ll always be more challenging: In cryptography, we have more opportunities to limit the harm of unintended exposure by preferring ephemeral keys over long-term ones, or at least rotating long-term keys periodically. Sadly, the closest analog of rotating keys I can think of in privacy is witness protection programs — a rather extreme and costly measure, and far from perfectly effective.
For privacy in the real world, the challenges of CoinJoin privacy remains.
This is an edited version of the article by @not_nothingmuch, posted on Spiral’s Substack June 11.
BM Big Reads are weekly, in-depth articles on some current topic relevant to Bitcoin and Bitcoiners. If you have a submission you think fits the model, feel free to reach out at editor[at]bitcoinmagazine.com.
This post How CoinJoin Anonymity Can Be Undermined Using Clustering first appeared on Bitcoin Magazine and is written by Yuval Kogman.
